мҡ°м„ н—ҘмӮ¬мҠӨнғҜ к°•нҷ”м—җ лҢҖн•ҙм„ңлҠ”В https://namu.wiki/w/HEXA%20%EB%A7%A4%ED%8A%B8%EB%A6%AD%EC%8A%A4#s-2.2 мқ„ м°ёмЎ°н•ҳмӢңкё° л°”лһҚлӢҲлӢӨ.
н—ҘмӮ¬мҠӨнғҜ к°•нҷ”лҘј к°„лӢЁнһҲ м„ӨлӘ… л“ңлҰ¬кІ мҠөлӢҲлӢӨ.
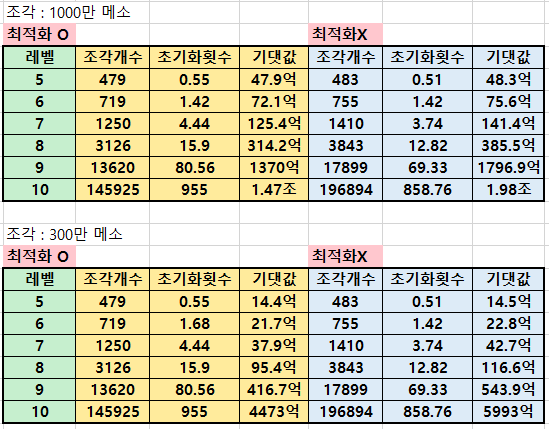
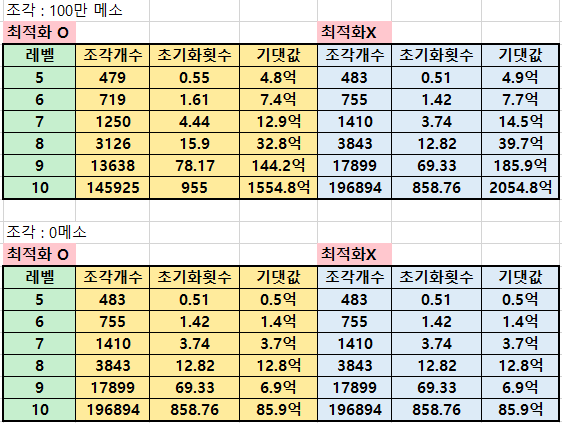
н—ҘмӮ¬мҠӨнғҜмқҖ л©”мқёмҠӨнғҜ н•ҳлӮҳмҷҖ л¶Җк°ҖмҠӨнғҜ 2к°ңлЎң мқҙлЈЁм–ҙ집лӢҲлӢӨ. к°Ғк°ҒмқҖ мөңлҢҖ 10л ҲлІЁк№Ңм§Җ к°•нҷ” лҗ мҲҳ мһҲмҠөлӢҲлӢӨ.
мҙқ 20лІҲмқҳ к°•нҷ”к°Җ 진н–үлҗҳкі к°Ғк°Ғмқҳ к°•нҷ”л§ҲлӢӨ л©”мқёмҠӨнғҜкіј л¶Җк°ҖмҠӨнғҜ 2к°ң мӨ‘ н•ҳлӮҳк°Җ лһңлҚӨмңјлЎң к°•нҷ”лҗ©лӢҲлӢӨ.
л©”мқёмҠӨнғҜмқҙ л¶Җк°ҖмҠӨнғҜліҙлӢӨ л§Һмқҙ мҳӨлҘҙкё° л•Ңл¬ём—җ л©”мқёмҠӨнғҜ 10л ҲлІЁмқ„ м°ҚлҠ” кІғмқҙ к°ҖмһҘ мўӢмҠөлӢҲлӢӨ.
10л“ұкёү мқҙмғҒл¶Җн„°лҠ”(мҙқ к°•нҷ” нҡҹмҲҳк°Җ 10лІҲ мқҙмғҒ) 1000л§Ң л©”мҶҢлҘј лӮҙкі мҠӨнғҜмқ„ мҙҲкё°нҷ” н• мҲҳ мһҲмҠөлӢҲлӢӨ.
м ңк°Җ н•ң мөңм Ғнҷ”лҠ” м–ҙл– н•ң кІҪмҡ°м—җ мҙҲкё°нҷ”лҘј н•ҙм•јм§Җ к°ҖмһҘ мўӢмқҖм§Җ кі„мӮ°н•ң кІғмһ…лӢҲлӢӨ.
мҳҲлҘј л“Өм–ҙ 10лІҲ к°•нҷ”н–ҲлҠ”лҚ° л©”мқёмҠӨнғҜм—җ н•ң лІҲлҸ„ л¶ҷм§Җ м•Ҡмңјл©ҙ мҙҲкё°нҷ”лҘј 진н–үн•©лӢҲлӢӨ.
мҳҶмқҳ л ҲлІЁмқҖ лӘ©н‘ңлЎң н•ҳлҠ” л©”мқёмҠӨнғҜмқҳ л ҲлІЁмқ„ мқҳлҜён•©лӢҲлӢӨ.
мөңм Ғнҷ”XлҠ” лӘ©н‘ң мҠӨнғҜм—җ лҸ„лӢ¬н• к°ҖлҠҘм„ұмқҙ мЎҙмһ¬л§Ң н•ңлӢӨл©ҙ мҙҲкё°нҷ” н•ҳм§Җ м•ҠлҠ” м „лһөмқ„ мӮ¬мҡ©н•ң кІҪмҡ°мһ…лӢҲлӢӨ.
(ex : лӘ©н‘ңмҠӨнғҜмқҙ 10мқҙкі 15к°•н–ҲлҠ”лҚ° 4к°• л¶ҷм—Ҳмңјл©ҙ лӮҳлЁём§Җ лӢӨ л¶ҷм–ҙлҸ„ 10мқҙ лҗ мҲҳ м—ҶмңјлҜҖлЎң мҙҲкё°нҷ”)
мөңм Ғнҷ”OлҠ” мөңм Ғ мҙҲкё°нҷ” л°©лІ•мқ„ мӮ¬мҡ©н•ң кІҪмҡ°мһ…лӢҲлӢӨ.
мҪ”л“ңлҠ” python кё°л°ҳ мҪ”л“ңлҘј мӮ¬мҡ©н•ҳмҳҖмҠөлӢҲлӢӨ. мЈјм„қмқ„ мқҪм–ҙліҙмӢңл©ҙ м–ҙл–Ө л°©мӢқмңјлЎң м§°лҠ”м§Җ мқҙн•ҙн•ҳмӢӨ мҲҳ мһҲмңјмӢӨ кІҒлӢҲлӢӨ.
нҳ№мӢң мһҳлӘ»лҗң м җ м°ҫмңјмӢңл©ҙ л§җм”Җ л¶ҖнғҒл“ңлҰҪлӢҲлӢӨ.
##н—ҘмӮ¬мҠӨн…ҹ к°•нҷ” мөңм Ғ м „лһө+кё°лҢ“к°’ нғҗмғүкё°
import numpy as np
import itertools
# nмқҖ нҳ„мһ¬ лӘҮ лІҲмқҳ к°•нҷ”к°Җ 진н–ү лҗҳм—ҲлҠ”м§ҖлҘј мқҳлҜён•Ё. мөңлҢҖ 20
# mмқҖ нҳ„мһ¬ main stat л ҲлІЁмқ„ мқҳлҜён•Ё. мөңлҢҖ 10
##### 1. кё°ліё мғҒмҲҳл“Ө
#p[m]мқҖ main statмқҙ mл ҲлІЁмқё мғҒнғңм—җм„ң к°•нҷ”лҘј н–Ҳмқ„ л•Ң main stat levelм—җ л¶ҷмқ„ нҷ•лҘ мқ„ мқҳлҜён•Ё. mмқҖ 0л¶Җн„° 10
p=np.array([0.35, 0.35, 0.35, 0.2, 0.2, 0.2, 0.2, 0.15, 0.1, 0.05, 0])
#s[m]мқҖ mлІҲ к°•нҷ”лҗң мғҒнғңм—җм„ң к°•нҷ”лҘј н–Ҳмқ„ л•Ң stat к°•нҷ”лҘј мң„н•ҙ н•„мҡ”н•ң мҶ”м—җлҘҙлӢӨ мЎ°к°Ғмқҳ к°ңмҲҳлҘј мқҳлҜён•Ё. mмқҖ 0л¶Җн„° 10
#лӮҳл¬ҙмң„нӮӨм—җ m=10мқј л•Ң к°’мқҙ м•Ҳ лӮҳмҷҖм„ң мқјлӢЁ мһ„мқҳлЎң 50 л„Јм—ҲмқҢ. 추нӣ„ мҲҳм •
s=np.array([10, 10, 10, 20, 20, 20, 20, 30, 40, 50, 50])
#crмқҖ мҙҲкё°нҷ” 비мҡ©мқ„ мқҳлҜён•Ё. лӢЁмң„лҠ” л§Ң л©”мҶҢмһ„. мҰү srмқҖ мІңл§Ң л©”мҶҢ
cr=1000
##### 2. мһ…л ҘмғҒмҲҳ
#csлҠ” мҶ”м—җлҘҙлӢӨмЎ°к°Ғ н•ҳлӮҳмқҳ л©”мҶҢк°ҖкІ©мқ„ мқҳлҜён•Ё. лӢЁмң„лҠ” л§Ң л©”мҶҢмһ„.
cs=1000
#oлҠ” лӘ©н‘ңлЎңн•ҳлҠ” main stat к°•нҷ” л ҲлІЁмқ„ мқҳлҜён•Ё. м–ҙм°Ён”ј 5мқҙмғҒмқҖ ліјкұ°лӢҲк№Ң 5л¶Җн„° 10к№Ңм§Җ л„Јмңјл©ҙ лҗЁ. мҳҲмҷёмІҳлҰ¬ к·Җм°®м•„....
o=10
##### 3 к°•нҷ” м „лһө м •мқҳ
#м „лһөмқҖ лӢӨмқҢкіј к°ҷмқҖ л°©мӢқмңјлЎң кІ°м •лҗЁ. nлІҲ к°•нҷ”н–Ҳмқ„ л•Ң main stat к°•нҷ”мҲҳм№ҳ m<=r[n]мқҙл©ҙ к°•нҷ”лҘј мӨ‘лӢЁн•ҳкі мІҳмқҢл¶Җн„° лӢӨмӢңмӢңмһ‘н•Ё
#r[n]мқҳ мЎ°кұҙл“ӨмқҖ м•„лһҳмҷҖ к°ҷмқҢ.
В В #3.1.1 -1<=r[n] // mмқҖ н•ӯмғҒ 0мқҙмғҒмқҙкё°л•Ңл¬ём—җ -1ліҙлӢӨ мһ‘мқҖ r[n]мқҖ м „л¶Җ лҳ‘к°ҷмқҢ.
В В #В В В В В В В В В к·ёлғҘ nлІҲ к°•нҷ” к№Ңм§ҖлҠ” м ҲлҢҖ нҸ¬кё°м•Ҳн• кұ°м•ј лқјлҠ” л§җмқҙ r[n]=-1мһ„. мҙҲкё°нҷ”к°Җ n>=10л¶Җн„° к°ҖлҠҘн•ҳлҜҖлЎң r[0~10]=-1лЎң к°Җм •н•Ё
В В #В В В В В В В В В м•„лһҳ 3.1.2~3.1.5лҠ” n>=10мқҙмғҒмқё кІҪмҡ°м—җл§Ң н•ҙлӢ№н•Ё.
В В #3.1.2 r[n]<o // к°•нҷ”к°Җ лӘ©н‘ң мҲҳм№ҳмқё oм—җ лҸ„лӢ¬н•ҳл©ҙ мҙҲкё°нҷ”н• н•„мҡ”к°Җ м—ҶмқҢ
В В #3.1.3 (o+n-21)<=r[n] // м•һмңјлЎң к°•нҷ”нҡҹмҲҳк°Җ (20-n)лІҲ лӮЁм•ҳлҠ”лҚ° лӢӨл¶ҷм–ҙлҸ„ лӘ©н‘ңмқё oм—җ лҸ„лӢ¬н• мҲҳ м—Ҷкё° л•Ңл¬ё/ мң„ мЎ°кұҙкіј н•©міҗм ё r[20]=0-1
В В #3.1.4 If n1<n2, then r[n1]<=r[n2] // 10лІҲмӨ‘ 5лІҲ л¶ҷмңјл©ҙ нҸ¬кё°н• кұҙлҚ° 11лІҲмӨ‘ 4лІҲ л¶ҷмқҖкұҙ нҸ¬кё°м•Ҳн•ҳл©ҙ мқҙмғҒн•ҳлӢҲк№Ң
В В #3.1.5 r[n+1]-r[n]=0 or 1 // 10лІҲмӨ‘ 4лІҲ л¶ҷмқҖкұҙ нҸ¬кё°м•Ҳн•ҳлҠ”лҚ° 11лІҲмӨ‘ 5лІҲ л¶ҷмқҖкұҙ нҸ¬кё°н• кұ°лқјлҠ”кІҢ л§җмқҙм•ҲлҗЁ
#мң„ мЎ°кұҙл“Өмқ„ л§ҢмЎұн•ҳлҠ” r[n]мқ„ мӨ‘ліөм—Ҷмқҙ лӘЁл‘җ кі лҘҙлҠ” л°©лІ•мқҖ лӢӨмқҢкіј к°ҷмқҢ
В В #3.1.7 мҡ°м„ r[10]к°’мқ„ кі лҰ„ мқҙ к°’мқ„ r10мқҙлқјкі н•ҳмһҗ. r10мқҳ лІ”мң„лҠ” -1<=r10<o мһ„.
В В #3.1.7 10л¶Җн„°19к№Ңм§Җмқҳ мҲ«мһҗмӨ‘ мӨ‘ліөм—Ҷмқҙ мҲңм„ңм—җ мғҒкҙҖм—Ҷмқҙ o-1-r10к°ңмқҳ мҲ«мһҗлҘј м„ нғқн•Ё. мқҙ мҲ«мһҗл“Өм—җ н•ҙлӢ№н•ҳлҠ” r[n+1]-r[n]=1лЎң л§Ңл“Өкұ°мһ„.
В В #3.1.8 к·ё мҲ«мһҗлҘј нҒ¬кё°к°Җ мһ‘мқҖмҲңмңјлЎң N[10],...,N[o+8-r10]лқјкі к°Җм •н•ҳмһҗ.
В В #3.1.9 r[0]~r[N[10]-10]=r10 && r[N[i]+1]~r[N[i+1]]=i+1+r10 for i=10,...,o-3-r10 && r[N[o-2-r10]+1]~r[10]=o-1
# мң„м—җм„ң л§җн•ңлҢҖлЎң nNк°ңмқҳ к°•нҷ” м „лһөмқҙ л§Ңл“Өм–ҙм§җ.
N=[]
for r10 in range(-1,o):
В В arr=[n for n in range(10,20)]
В В Nm=list(itertools.combinations(arr,o-r10-1))
В В N.extend(Nm)
nN=len(N)
##л¬ҙм§Җм„ұ к°•нҷ” м •мқҳ: main statмқҙ oк°•м—җ лҸ„лӢ¬н• к°ҖлҠҘм„ұмқҙ мЎҙмһ¬л§Ң н•ңлӢӨл©ҙ л¬ҙмЎ°кұҙ к°•нҷ”н•ҳлҠ” кІғмқ„ мқҳлҜё(결과비көҗмҡ©)
rm=[o-1-20+n if n>=20-o+1 else -1 for n in range(21)]
##### 4 к°•нҷ” м „лһөлі„ кё°лҢ“к°’ нғҗмғү мӢңмһ‘
##cлҠ” к°•нҷ”м „лһөлі„ мҶҢлӘЁл©”мҶҢ кё°лҢ“к°’мқ„ мқҳлҜён•Ё. лӮҳмӨ‘м—җ мөңм Ғмқҳ к°•нҷ”м „лһөмқ„ м°ҫкё° мң„н•ҙ мӮ¬мҡ©. мҡ°м„ мқҖ мҙҲкё°нҷ”
##rnмқҖ к°•нҷ”м „лһөлі„ мҙҲкё°нҷ” нҡҹмҲҳ кё°лҢ“к°’мқ„ мқҳлҜён•Ё.
##rnмқҖ к°•нҷ”м „лһөлі„ мҶ” м—җлҘҙлӢӨ мЎ°к°Ғмқҳ мҶҢлӘЁ кё°лҢ“к°’мқ„ мқҳлҜён•Ё.
c=np.zeros(nN)
rn=np.zeros(nN)
sn=np.zeros(nN)
for i in range(nN):
В В ##4.1 к°•нҷ” м „лһө N[i]лЎң л¶Җн„° r[n]мқ„ мғқм„ұ (3.1.9 м°ёмЎ°)
В В r10=o-len(N[i])-1
В В Ni=np.array(N[i])
В В r=np.array([-1 for n in range(21)],dtype=int)
В В if Ni.shape[0]==0:
В В В В for j in range(10,21):
В В В В В В r[j]=r10
В В else:В В В В
В В В В for j in range(10,Ni[0]+1):
В В В В В В r[j]=r10
В В В В for j in range(0,o-2-r10):
В В В В В В for k in range(Ni[j]+1,Ni[j+1]+1):
В В В В В В В В r[k]=r10+j+1
В В В В for j in range(Ni[o-2-r10]+1,21):
В В В В В В r[j]=o-1
В В В В В В В
В В ##ліё л°©лІ•мқҙ л¬ҙм§Җм„ұ к°•нҷ”м—җ н•ҙлӢ№н•ҳлҠ”м§Җ мІҙнҒ¬
В В if list(r)==rm:
В В В В im=i
В В В
В В ##4.2 к°•нҷ” м „лһө N[i]лЎң лӘ©н‘ң oлҘј лӢ¬м„ұн•ҳлҠ”лҚ° мҶҢлӘЁн•ҳлҠ” л©”мҶҢмқҳ кё°лҢ“к°’ кі„мӮ°
В В #cm[n][m]мқ„ нҳ„мһ¬ nлІҲк°•нҷ”м—җм„ң mлІҲ main statм—җ л¶ҷмқҖмғҒнҷ©мқҙкі , м—¬кё°м„ң к°•нҷ”лҘј 진н–үн•ҙ лӘ©н‘ңлҘј лӢ¬м„ұн• л•Ңк№Ңм§Җмқҳ мҶҢлӘЁл©”мҶҢ кё°лҢ“к°’мқҙлқј н•ҳмһҗ.
В В #мқҙл•Ң n<=10мқёкІҪмҡ° 0<=m<=nмқҙлӢӨ.
В В #к·ёлҰ¬кі n>=11мқёкІҪмҡ° max(0,r[n])<=m<=10мқҙлӢӨ. к°•нҷ”м „лһө мғҒ лӢӨлҘё кІҪмҡ°лҠ” мқҙлҜё мҙҲкё°нҷ”н•ҙлІ„л ёкё° л•Ңл¬ём—җ мЎҙмһ¬н• мҲҳ м—ҶмқҢ
В В #мң„м—җм„ң мҷјмӘҪ л“ұнҳёлҠ” nмқҙ N[i]мқҳ мӣҗмҶҢмқјл•Ңл§Ң к°ҖлҠҘ мҷңлғҗн•ҳл©ҙ 10к°ңмӨ‘ 5к°ңлҘј мҙҲкё°нҷ”н–ҲлӢӨл©ҙ 11к°ңмӨ‘ 5к°ңмқё мғҒнҷ©мқҖ лӮҳмҳ¬ мҲҳ м—Ҷкё° л•Ңл¬ё.
В В ##r2[n]кіј r3[n]мқҖ мң„ мЎ°кұҙл“Өмқ„ кі л Өн•ҳм—¬ к°ҖлҠҘн•ң (n,m)мқҳ мЎ°н•©мқҙ r2[n]<=m<=r3[n]мқҙ лҗҳлҸ„лЎқ л§Ңл“ мӢқмқҙлӢӨ.
В В r2=np.zeros(21,dtype=int)
В В r3=np.array([np.min([10,n]) for n in range(21)])
В В r2[11:21]=r[11:21]+1
В В for j in range(o-1-r10):
В В В В r2[Ni[j]+1]-=1
В В
В В ##4.3 к°•нҷ” м „лһө N[i]лЎң лӘ©н‘ң oлҘј лӢ¬м„ұн•ҳлҠ”лҚ° мҶҢлӘЁн•ҳлҠ” л©”мҶҢмқҳ кё°лҢ“к°’ кі„мӮ°
В В #м„ёк°Җм§ҖкІҪмҡ°лҘј мғқк°Ғн•ҳмһҗ.
В В #(n>10 and m=r[n]мқё кІҪмҡ°) or (n=10 m<r[10])мқё кІҪмҡ°)(4.3.1)мҷҖ (20,m>=o)мқё кІҪмҡ°(4.3.2)мҷҖ n<19мқҙкі r[n]<m<=r3[n]мқё кІҪмҡ°(4.3.3)
В В В #4.3.1 cm[n][m]=cr+cm[0][0] /мҙҲкё°нҷ”лҘј н•ҳкі лӢӨмӢң (n,m)=(0,0)мқё кІҪмҡ°лЎң к°Җкё° л•Ңл¬ё
В В В #4.3.2 cm[20][m]=0 /лӘ©н‘ңлҘј мқҙлҜё лӢ¬м„ұн–Ҳкё°л•Ңл¬ём—җ кё°лҢ“к°’мқҖ 0.
В В В #4.3.3 cm[n][m]=cs*s[m]+cm[n+1][m+1]*p[m]+cm[n+1][m]*(1-p[m]) /м„ӨлӘ…мқҖ л°‘ м°ёмЎ°. (cm[n+1][11]мқҖ м–ҙм°Ён”ј p[10]=0мқҙлҜҖлЎң кі л Өм•Ҳн•Ё)В
В В В #мІ«лІҲм§ё termмқҖ к°•нҷ”비мҡ©
В В В #л‘җлІҲм§ё termмқҖ м„ұкіөн•ҳлҠ” кІҪмҡ°
В В В #м„ёлІҲм§ё termмқҖ мӢӨнҢЁн•ҳлҠ” кІҪмҡ°
В В #мң„ м—°лҰҪ л°©м •мӢқмқ„ м—°лҰҪн•ҙм„ң cm[0][0]мқ„ кі„мӮ°н•ҳл©ҙ лҗЁ.
В В #мң„ м—°лҰҪ л°©м •мӢқмқ„ н–үл ¬мқ„ мқҙмҡ©н•ҙм„ң н’Җкё° мң„н•ҙ reindexingмқ„ 진н–үн•ҳкІ мқҢ. (n,m)мқ„ kлЎң лҢҖмқ‘мӢңмјң cm[n][m]мқ„ cmk[k]лЎң ліҖнҷҳ
В В #ktonm[k]=[n,m],nmtok[n,m]=k, ksлҠ” мҙқ kмқҳ к°ңмҲҳ
В В #4.3.1, 4.3.2, 4.3.3лЎң мқҙлЈЁм–ҙ진 м—°лҰҪл°©м •мӢқмқ„ cmk=A*cmk+bлЎң ліҖнҷҳ.
В В nmtok=np.zeros([21,11],dtype=int)
В В ktonm=[]
В В kindex=0
В В for n in range (0,21):
В В В В for m in range(r2[n],r3[n]+1):
В В В В В В nmtok[n][m]=kindex
В В В В В В ktonm.append([n,m])
В В В В В В kindex+=1
В В A=np.zeros([kindex,kindex])
В В b=np.zeros([kindex])
В В В
В В В
В В ##4.4мҙҲкё°нҷ” нҡҹмҲҳмқҳ кё°лҢ“к°’ кі„мӮ°
В В #rnm[n][m]мқ„ л©”мҶҢмқҳ кё°лҢ“к°’кіј 비мҠ·н•ң л°©мӢқмңјлЎң м•һмңјлЎң мҙҲкё°нҷ”н• нҡҹмҲҳмқҳ кё°лҢ“к°’мқҙлқј к°Җм •
В В #мң„мҷҖ лҳ‘к°ҷмқҙ м„ёк°Җм§ҖкІҪмҡ°лҘј мғқк°Ғн•ҳмһҗ.
В В #(n>10 and m=r[n]мқё кІҪмҡ°) or (n=10 m<r[10])мқё кІҪмҡ°)(4.3.1)мҷҖ (20,m>=o)мқё кІҪмҡ°(4.3.2)мҷҖ n<19мқҙкі r[n]<m<=r3[n]мқё кІҪмҡ°(4.3.3)
В В В #4.4.1 rnm[n][m]=1+rnm[0][0]
В В В #4.4.2 rnm[20][m]=0В
В В В #4.4.3 rnm[n][m]=rnm[n+1][m+1]*p[m]+rnm[n+1][m]*(1-p[m])
В В #мң„ м—°лҰҪ л°©м •мӢқмқ„ м—°лҰҪн•ҙм„ң rnm[0][0]мқ„ кі„мӮ°н•ҳл©ҙ лҗЁ. reindexing лҳ‘к°ҷмқҙн•ҙм„ң rnmkлҸ„ л§Ң듬
В В #4.4.1, 4.4.2, 4.4.3лЎң мқҙлЈЁм–ҙ진 м—°лҰҪл°©м •мӢқмқ„ rnmk=A*rnmk+b2лЎң ліҖнҷҳ.В (Aн–үл ¬мқҖ лҸҷмқјн•Ё)
В В В
В В b2=np.zeros([kindex])
В В В
В В ##4.5мӮ¬мҡ© мЎ°к°Ғ мҲҳмқҳ
В В #snm[n][m]мқ„ л©”мҶҢмқҳ кё°лҢ“к°’кіј 비мҠ·н•ң л°©мӢқмңјлЎң м•һмңјлЎң мҙҲкё°нҷ”н• нҡҹмҲҳмқҳ кё°лҢ“к°’мқҙлқј к°Җм •
В В #мң„мҷҖ лҳ‘к°ҷмқҙ м„ёк°Җм§ҖкІҪмҡ°лҘј мғқк°Ғн•ҳмһҗ.
В В #(n>10 and m=r[n]мқё кІҪмҡ°) or (n=10 m<r[10])мқё кІҪмҡ°)(4.3.1)мҷҖ (20,m>=o)мқё кІҪмҡ°(4.3.2)мҷҖ n<19мқҙкі r[n]<m<=r3[n]мқё кІҪмҡ°(4.3.3)
В В В #4.5.1 snm[n][m]=snm[0][0]
В В В #4.5.2 snm[20][m]=0В
В В В #4.5.3 snm[n][m]=s[m]+snm[n+1][m+1]*p[m]+snm[n+1][m]*(1-p[m])
В В #мң„ м—°лҰҪ л°©м •мӢқмқ„ м—°лҰҪн•ҙм„ң snm[0][0]мқ„ кі„мӮ°н•ҳл©ҙ лҗЁ. reindexing лҳ‘к°ҷмқҙн•ҙм„ң snmkлҸ„ л§Ң듬
В В #4.5.1, 4.5.2, 4.5.3лЎң мқҙлЈЁм–ҙ진 м—°лҰҪл°©м •мӢқмқ„ snmk=A*snmk+b3лЎң ліҖнҷҳ.В (Aн–үл ¬мқҖ лҸҷмқјн•Ё)В В
В В В
В В b3=np.zeros([kindex])
В В В
В В ##AмҷҖ b, b2, b3лҘј мһ‘м„ұ.
В В for n in range (0,21):
В В В В В
В В В В ## (4.3.1)
В В В В #(n,m=r[n])мқҙ к°ҖлҠҘн•ң кІҪмҡ°мқём§Җ мІҙнҒ¬н•ҳкё° мң„н•ҙ мЎҙмһ¬н•Ё (0,0)лҸ„ к°ҖлҠҘн•ҳм§Җл§Ң м–ҙм°Ён”ј мҙҲкё°нҷ” м•Ҳн• кұ°лқј мғҒкҙҖм—ҶмқҢ.
В В В В if nmtok[n][r[n]]!=0:
В В В В В В if n!=10:
В В В В В В В В if r[n]!=-1:
В В В В В В В В В В A[nmtok[n][r[n]]][0]=1
В В В В В В В В В В b[nmtok[n][r[n]]]=cr
В В В В В В В В В В b2[nmtok[n][r[n]]]=1
В В В В В В else:
В В В В В В В В for m in range(0,r10+1):
В В В В В В В В В В A[nmtok[n][m]][0]=1
В В В В В В В В В В b[nmtok[n][m]]=crВ В В В В В В В В В В
В В В В В В В В В В b2[nmtok[n][m]]=1В В
В В В В В
В В В В ## (4.3.2) ліҖкІҪн• кІғ м—ҶмқҢ.
В В В В В
В В В В ## (4.3.3)
В В В В if n!=20:
В В В В В В for m in range(r[n]+1,r3[n]+1):
В В В В В В В В if m!=10:
В В В В В В В В В В A[nmtok[n][m]][nmtok[n+1][m+1]]=p[m]
В В В В В В В В A[nmtok[n][m]][nmtok[n+1][m]]=1-p[m]
В В В В В В В В b[nmtok[n][m]]=cs*s[m]
В В В В В В В В b3[nmtok[n][m]]=s[m]
В В В В В В В В В
В В #cmk=inv(I-A)*b
В В inv=np.linalg.inv(np.eye(kindex)-A)
В В cmk=inv.dot(b)
В В rnmk=inv.dot(b2)
В В snmk=inv.dot(b3)
В В c[i]=cmk[0]
В В rn[i]=rnmk[0]
В В sn[i]=snmk[0]
В В #кі„мӮ° 진н–ү нҷ•мқёмҡ©.
#В В if i%10000==0:
#В В В В print(round((i/nN)*100,1),'% кі„мӮ°мҷ„лЈҢ')
####5. кі„мӮ° кІ°кіјлҘј нҶөн•ҙ мөңм Ғ м „лһө м¶ңл Ҙ
##л¬ҙм§Җм„ұ к°•нҷ”лһҖ main statмқҙ oк°•м—җ лҸ„лӢ¬н• к°ҖлҠҘм„ұмқҙ мЎҙмһ¬л§Ң н•ңлӢӨл©ҙ л¬ҙмЎ°кұҙ к°•нҷ”н•ҳлҠ” кІғмқ„ мқҳлҜё
print('лӘ©н‘ң лҸ„лӢ¬ к°ҖлҠҘм„ұл§Ң мһҲмңјл©ҙ л¬ҙм§Җм„ұ к°•нҷ”мӢң',round(c[im]/10000,1),'м–өл©”мҶҢ')
print('лӘ©н‘ң лҸ„лӢ¬ к°ҖлҠҘм„ұл§Ң мһҲмңјл©ҙ л¬ҙм§Җм„ұ к°•нҷ”мӢң мҙҲкё°нҷ” нҡҹмҲҳ', round(rn[im],2))
print('лӘ©н‘ң лҸ„лӢ¬ к°ҖлҠҘм„ұл§Ң мһҲмңјл©ҙ л¬ҙм§Җм„ұ к°•нҷ”мӢң мЎ°к°Ғ к°ҜмҲҳ', round(sn[im],2))
print('мөңм Ғм „лһө мӮ¬мҡ©мӢң',round(c.min()/10000,1),'м–өл©”мҶҢ')
oi=c.argmin()
print('мөңм Ғм „лһө мӮ¬мҡ©мӢң мҙҲкё°нҷ” нҡҹмҲҳ', round(rn[oi],2))
print('мөңм Ғм „лһө мӮ¬мҡ©мӢң мЎ°к°Ғ к°ҜмҲҳ', round(sn[oi],2))
r10=o-len(N[oi])-1
Ni=np.array(N[oi])
r=np.array([-1 for n in range(21)],dtype=int)
if Ni.shape[0]==0:
В В for j in range(10,21):
В В В В r[j]=r10
else:В В В В
В В for j in range(10,Ni[0]+1):
В В В В r[j]=r10
В В for j in range(0,o-2-r10):
В В В В for k in range(Ni[j]+1,Ni[j+1]+1):
В В В В В В r[k]=r10+j+1
В В for j in range(Ni[o-2-r10]+1,21):
В В В В r[j]=o-1
print('мөңм Ғм „лһө')
if r[10]!=-1:
В В print('10 лІҲ к°•нҷ”мӢң к°•нҷ” лӢЁкі„к°Җ', r[10], 'мқҙн•ҳл©ҙ мҙҲкё°нҷ”')
for i in range(Ni.shape[0]):
В В print(Ni[i]+1,'лІҲ к°•нҷ”мӢң к°•нҷ” лӢЁкі„к°Җ',r[Ni[i]+1],'мқҙл©ҙ мҙҲкё°нҷ”')
4. н•ң мӨ„ мҡ”м•Ҫ
мЎ°к°Ғ л„Ҳл¬ҙ 비мӢёлӢӨ. мЎ°к°Ғ л“ңлһҚлҘ мғҒн–Ҙ мўҖ.