자주포의 탄착군에 대해서 알아보려 합니다.
가까운 거리에서는 탄착군이 위아래로 길게 되는 반면 중간보다 좀 더 먼지점에서는 원이되고 최대사거리에서는 좌우로만 탄착군이 형성되는걸 볼 수 있습니다. 왜그런지 봅시다.
일단 정확한 각도로 쐈을때를 먼저 봅시다.
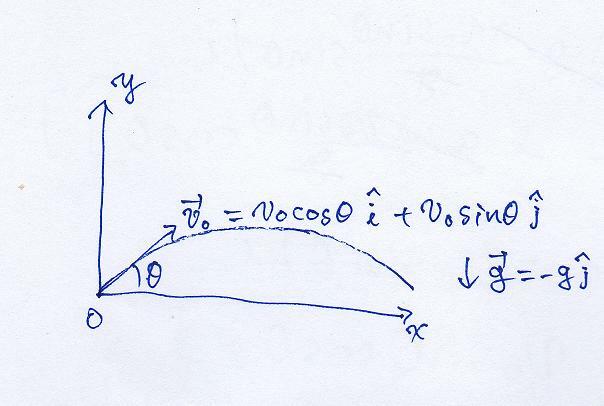
볼드체는 벡터이고,
i,
j,
k는 x축, y축, z축의 단위벡터입니다.
다음과 같은 식이 성립됩니다.
F = m
a = m
g = -mg
j (
g = -g
j)
->
a = -g
j (
a = d
v/dt = d^2
r/dt^2)
이것으로부터
v = v(0)cosθ
i + [v(0)sinθ - gt]
j (
v(0) = v(0)cosθ
i+ v(0)sinθ
j)
r = v(0)tcosθ
i + [v(0)tsinθ - 0.5gt^2]
j땅에 닿는 시간 t(
s) = [2v(0)sinθ]/g
도달거리
s(θ) = [((v(0)^2)sin2θ)/g]
i그런데, 알겠지만 정확하게 저 지점으로 떨어지지 않습니다. 왜냐하면 탄이 포에서 나갈때 약간의 오차를 가지고 날아가기 때문입니다. 위아래는 각도(elevation angle)에 대한 오차가 있고 좌우로도 각도에 대해 오차가 있습니다. 그 오차를 각각 Δθ, Δφ라고 합시다.
Δθ에 대해서 도달거리를 벡터로 구하면
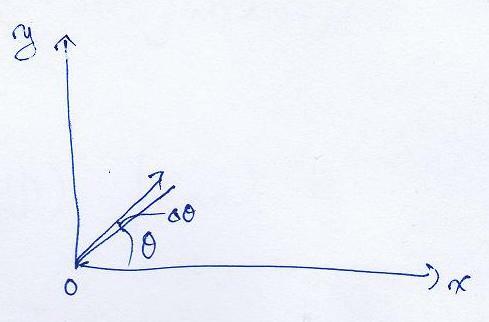 s
s(θ+Δθ) = [((v(0)^2)sin2(θ+Δθ))/g]
iΔφ에 대해서도 같이 구해주면
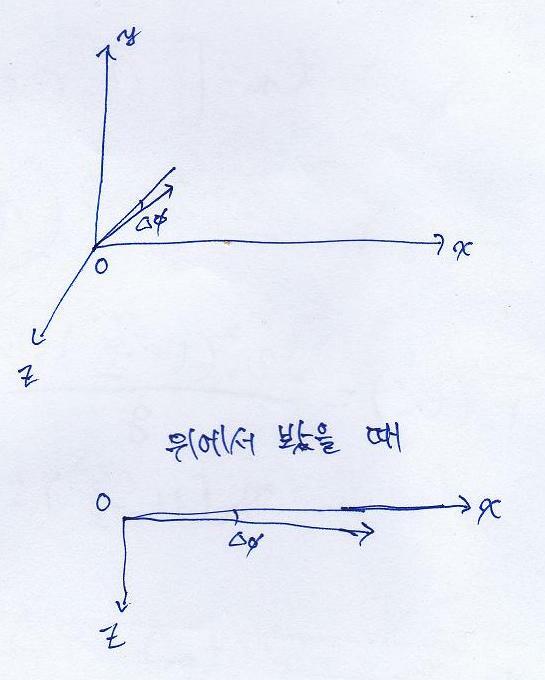 s
s(θ,Δφ) = [((v(0)^2)sin2θ)/g]
i +
[(2(v(0)^2)Δφsinθ)/g]
k탄착군의 위아래와 좌우경계(boundary)는 Δθ, Δφ가 각각 최대일때 나타납니다. 또 월탱에서는 발사시 오차가 원으로 생기므로 그 두 값은 같습니다. 따라서 Δθ = Δφ = δ로 놓고, δ가 작다고 가정하고 first order까지 expansion 해주면
Δθ만큼 변했을 때 탄착군의 위아래 경계는
s(θ+Δθ) -
s(θ) = [(2(v(0)^2)δcos2θ)/g]
i
Δφ만큼 변했을 때의 탄착군의 좌우 경계는
s(θ,Δφ) -
s(θ) = [(2(v(0)^2)δsinθ)/g]
k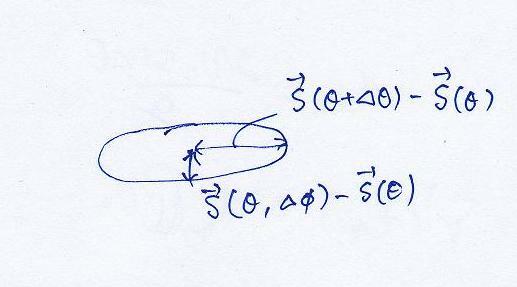
위아래와 좌우의 비율은
|
s(θ+Δθ) -
s(θ)|/|
s(θ,Δφ) -
s(θ)| = cos2θ/sinθ = 1/sinθ - 2sinθ
따라서
탄착군은 θ값이 작으면 위아래(i방향)로 길게 생기며 최대사거리일땐 위아래가 0 이 됩니다. (cos2θ = 0 이므로)
s(θ,Δφ) -
s(θ) = t(
s)v(0)Δφ
k 이므로
좌우로는(k방향) 탄이 비행하는 시간에 비례합니다. (이건 계산 안해도 짐작하겠죠?)
탄착군이 원형이 되는 지점은 위아래/좌우 = 1 일때이므로,
sinθ = cos2θ
-> θ = sin^(-1)(1/2) = 30도
탄착군이 원이 되는 발사각은 30도이고 그때의 거리와 최대사거리의 비율은 sin(60도)/sin(90도) = (3^0.5)/2 = 0.866
즉
최대사거리의 약 0.87배가 되는 지점에서 탄착군이 원이 되는걸 알 수 있습니다.공기저항이 들어간다면 이 식은 굉장히 복잡해질거라 생각됩니다만, 공기저항을 고려하지 않고서도 비스무리한 결론이 나온다는게 다행스럽네요.
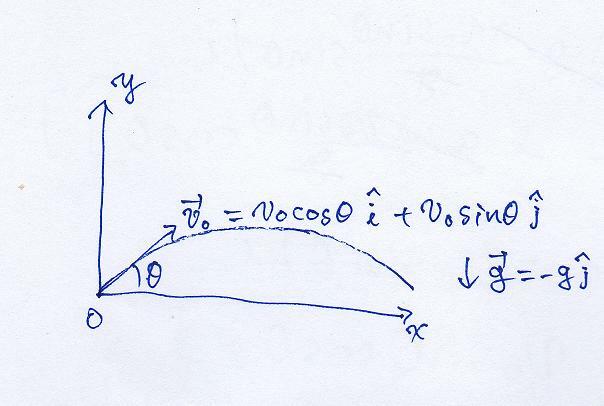



 beautyboy
beautyboy
