мӣҗм№ҙл“ң мҪ”мқё мҠөл“қм—җ лҢҖн•ҳм—¬ кёҖмқ„ м“°кІҢ лҗҳм—ҲмҠөлӢҲлӢӨ.
(м»ҙн“Ён„° нҷ”л©ҙм—җ мөңм Ғнҷ”лҗҳм–ҙ мһҲмҠөлӢҲлӢӨ)
мқҙлІҲ мӣҗм№ҙл“ң мҪ”мқё мҲҳкёүмқҖ л§Өмҡ° ліөмһЎн•ң л°©мӢқмңјлЎң кө¬лҸҷлҗҳлҠ”кІғ к°ҷмҠөлӢҲлӢӨ.
мӢңк°„м—җ л”°лқј мҪ”мқёмқ„ мЈјкі , л“ұмҲҳм—җ л”°лқј мҪ”мқёмқ„ мЈјкі , мӢ¬м§Җм–ҙ 4л“ұмқҖ мҪ”мқёмЎ°м°Ё мЈјм§Җ м•ҠлҠ” г…— кө¬мЎ°.
мқҙ кө¬мЎ°к°Җ м–ҙл–»кІҢ кө¬лҸҷлҗҳлҠ”м§Җ нҢҢм•…н•ҳкё° мң„н•ҙ м ҖлҠ” м—¬лҹ¬ к°Җм„Өмқ„ м„Өм •н–ҲмҠөлӢҲлӢӨ.
лӢ№м—°нһҲ м •нҷ•н•ҳм§Җ м•ҠмқҢмңјлЎң к·ёлғҘ к°ҖліҚкІҢ лҙҗ мЈјмӢңл©ҙ к°җмӮ¬л“ңлҰ¬кІ мҠөлӢҲлӢӨ~~~
мҡ°м„ , мқҙ мӢӨн—ҳмқ„ мң„н•ҙ мӢ лў°кө¬к°„ 90%м—җ мҳӨм°ЁлІ”мң„ 5%лЎң н‘ңліё 271к°ңлҘј 추м¶ңн–ҲмҠөлӢҲлӢӨ. м—¬кё°м„ң 4л“ұн•ң кІҪмҡ°лҠ” м ңмҷён•ҳмҳҖмҠөлӢҲлӢӨ. мһҗлЈҢлҠ” мҪ”мқёмҠөл“қлҹү, мӣҗм№ҙл“ңн•ңмӢңк°„, л°© мқёкө¬мҲҳ, л“ұмҲҳлҘј мёЎм •н•ҳмҳҖмҠөлӢҲлӢӨ.
м—¬кё°м„ң мӣҗм№ҙл“ң н•ң мӢңк°„мқҙ л§Өмҡ° м• л§Өн•©лӢҲлӢӨ... м ң м»ҙн“Ён„°к°Җ мқҙмғҒн•ңм§Җ мӣҗкё°к°Җ мқҙмғҒн•ңм§Җ мӢңк°„ нғҖмқҙлЁёк°Җ м—Ҷм–ҙмЎҢлӢӨ л“ұмһҘн–ҲлӢӨ н•ҙм„ң...
мӢңк°„н‘ңмӢңк°Җ м—ҶлӢӨ;;
к·ёлһҳм„ң м ңк°Җ м§Ғм ‘ мӣҗм№ҙл“ң м№ҙл“ңлҘј л°°л¶Җн•ң мҲңк°„л¶Җн„° лҒқлӮң мӢңк°„к№Ңм§Җмқҳ мӢңк°„мқ„ м§Ғм ‘ мёЎм •н•ҳмҳҖмҠөлӢҲлӢӨ.
к·ёл Үкё°м—җ мӢӨм ң л°© мһ…мһҘл¶Җн„° мӣҗм№ҙл“ңк°Җ лҒқлӮң кё°к°„мқҖ лӢ№м—°нһҲ м ңк°Җ мёЎм •н•ң мӢңк°„ліҙлӢӨ мқјм • мӢңк°„ лҚ” кёё мҲҳ л°–м—җ м—ҶмҠөлӢҲлӢӨ.
н•ҳм§Җл§Ң мқҙ мӢңк°„мқҖ м „л¶Җ мқјм •н•ң мӢңк°„мқ„ к°Җм§Җкё°м—җ л¬ём ңк°Җ м—ҶлӢӨкі нҢҗлӢЁн•ҳм—¬ к·ёлғҘ м ңк°Җ мёЎм •н–ҲмҠөлӢҲлӢӨ.
мһҗ к·ёл ҮлӢӨл©ҙ!
1. мҪ”мқё(C)мқҖ мӢңк°„(t), л°© мқёкө¬мҲҳ(1лҢҖ3, 1лҢҖ2, 1лҢҖ1мқ„ л§җн•Ё; P), л“ұмҲҳ(R)м—җ к°Ғк°Ғ мҳҒн–Ҙмқ„ л°ӣлҠ”к°Җ?
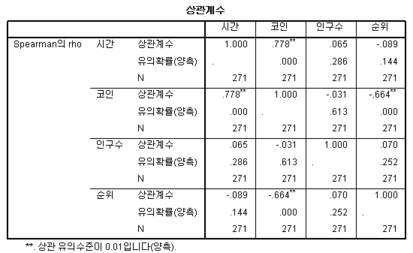
мқҙм—җ лҢҖн•ҙ мғҒкҙҖм„ұмқ„ кө¬н•ҳкі мһҗ мҠӨн”јм–ҙл§Ң мғҒкҙҖкі„мҲҳлҘј кө¬н–ҲмҠөлӢҲлӢӨ. мҷң н”јм–ҙмҠЁмқҙ м•„лӢҢ мҠӨн”јм–ҙл§ҢмңјлЎң н•ҳмҳҖлӮҳл©ҙ, м„ нҳ•м„ұмқҙ мһҲлҠ”м§Җмқҳ м—¬л¶ҖлҘј м ңмҷён•ҳкі лӢЁмЎ°м Ғмқё кҙҖкі„к°Җ мһҲлҠ”м§ҖлҘј м•Ңкі мӢ¶м—Ҳкё° л•Ңл¬ёмһ…лӢҲлӢӨ. к·ё кІ°кіј мҪ”мқё, мӢңк°„, л“ұмҲҳл§Ң м„ңлЎң мғҒкҙҖм„ұмқ„ к°Җм§ҖлҠ” кІғмқ„ м•Ң мҲҳ мһҲмҠөлӢҲлӢӨ. мҰү, л°© мқёкө¬мҲҳмҷҖ лі„к°ңлЎң к·ёлғҘ л“ұмҲҳк°Җ лҶ’мңјл©ҙ мҪ”мқёмқ„ л§Һмқҙ мЈјлҠ” кІғмқҙмЈ .
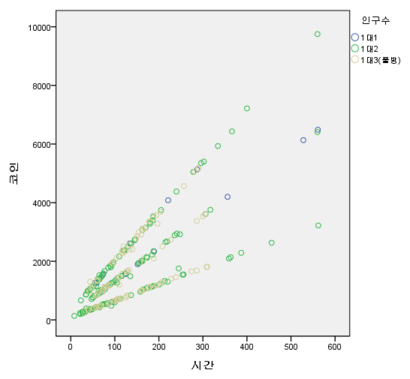
мӮ°нҸ¬лҸ„лҘј ліҙлҚ”лқјлҸ„ л°© мқёкө¬мҲҳлҠ” лі„лЎң мғҒкҙҖм—Ҷкі л“ұмҲҳм—җ л”°лқј нҢЁн„ҙмқҙ мһҲмқҢмқ„ м•Ң мҲҳ мһҲмҠөлӢҲлӢӨ.
2. к·ёл ҮлӢӨл©ҙ мҪ”мқё(C)кіј мӢңк°„(t)кіј л“ұмҲҳ(R)мқҖ м–ҙл–Ө кҙҖкі„лҘј к°Җм§ҖлҠ”к°Җ?
лӢӨн–үмқҙлҸ„ мҪ”мқёкіј мӢңк°„м—җ кҙҖн•ҙм„ңлҠ” 1м°Ёмқҳ м„ нҳ•кҙҖкі„лҘј к°Җм§ҖлҠ” кІғмңјлЎң лӮҳнғҖлӮ¬мҠөлӢҲлӢӨ. мҰү, л№„м„ нҳ•мқҙ м•„лӢҲкё° л•Ңл¬ём—җ нҺён•ҳкІҢ мҪ”мқёмқ„ лӘЁмңјл©ҙ лҗ©лӢҲлӢӨ.
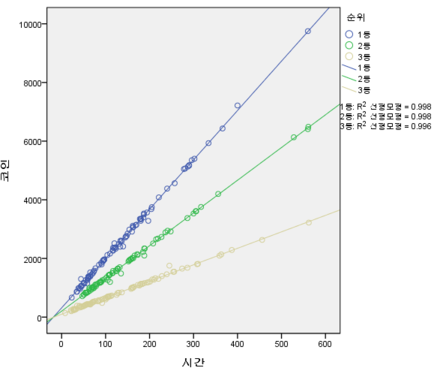
лӢӨмқҢмқҖ, мҪ”мқёкіј мӢңк°„кіј л“ұмҲҳм—җ кҙҖн•ҳм—¬ мҙҲлӢ№ мҪ”мқё нҸ¬мқёнҠё(100нҸ¬мқёнҠёлӢ№ 1мҪ”мқёмһ„)мқ„ м–»мқ„ мҲҳ мһҲлҠ” "мҪ”мқён•ЁмҲҳ"лҘј м¶”лЎ н•ҳмҳҖлӢӨ. мҪ”мқён•ЁмҲҳ C(t, R)м—җм„ң tлҠ” мӢңк°„, RмқҖ л“ұмҲҳмһ…лӢҲлӢӨ.
1л“ұм—җ лҢҖн•ҳм—¬ мҪ”мқён•ЁмҲҳлҠ”В В В "C(t, 1)=16.825t + 315.724"В В В (tм—җ кҙҖн•ҳм—¬ 90% мӢ лў°кө¬к°„мқҖ (16.69,16.96))
2л“ұм—җ лҢҖн•ҳм—¬ мҪ”мқён•ЁмҲҳлҠ”В В В "C(t, 2)=11.154t + 205.283"В В В (tм—җ кҙҖн•ҳм—¬ 90% мӢ лў°кө¬к°„мқҖ (11.063,11.246))
3л“ұм—җ лҢҖн•ҳм—¬ мҪ”мқён•ЁмҲҳлҠ”В В В "C(t, 3)=5.616t + 100.104"В В В В (tм—җ кҙҖн•ҳм—¬ 90% мӢ лў°кө¬к°„мқҖ (5.554,5.678))
4л“ұмқҖ лӢ№м—°нһҲ 0к°ңмһ…лӢҲлӢӨ(C(t, 4)=0).
(нҡҢк·Җ분м„қм—җм„ң 1л“ұмқҖ R^2=.998, 2л“ұмқҖ R^2=.998, 3л“ұмқҖ R^2=.996мңјлЎң кІ°м •кі„мҲҳк°Җ л§Өмҡ° лҶ’м•ҳлӢӨ. к·ёлҰ¬кі м „л¶Җ P=.000мңјлЎңВ Оұ<0.001 мҲҳмӨҖм—җм„ң мң мқҳлҜён•ң кІғмңјлЎң лӮҳнғҖлӮЁ.)
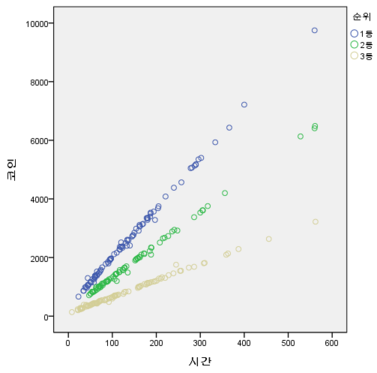
к·ёл ҮлӢӨл©ҙ, л“ұмҲҳм—җ лҢҖн•ҳм—¬ л“ұк°„м„ұмқҙ мһҲлҠ”м§ҖлҘј мӮҙнҺҙліҙмһҗ. м—¬кё°м„ң л“ұк°„м„ұмқҖ 3л“ұ, 2л“ұ, 1л“ұмқҳ кё°мҡёкё°к°Җ м„ңлЎң мқјм •н•ң нҢЁн„ҙмқ„ к°Җм§ҖлҠ”к°Җ?
1л“ұкіј 2л“ұм—җ лҢҖн•ң 비мңЁмқҖ м•Ҫ 66.3%лЎң лӮҳнғҖлӮ¬мҠөлӢҲлӢӨ. к·ёлҰ¬кі 1л“ұкіј 3л“ұм—җ лҢҖн•ң 비мңЁмқҖ м•Ҫ 33.38%лЎң лӮҳнғҖлӮ¬мҠөлӢҲлӢӨ. мқҙлҘј нҶөн•ҙ мҡ°лҰ¬лҠ” мҳӨм°ЁлІ”мң„лҘј к°җм•Ҳн•ҳм—¬ лҢҖлһө 1л“ұ лҢҖ비 2л“ұмқҖ 66.6%, 3л“ұмқҖ 33.3%мқҳ мҪ”мқёмқ„ мҠөл“қн•ңлӢӨкі ліј мҲҳ мһҲмҠөлӢҲлӢӨ.В
мҰү, л“ұмҲҳмҷҖ кҙҖл Ён•ҳм—¬ мҪ”мқёлі„ мҠөл“қлҹүмқҖ л“ұк°„м„ұмқ„ к°Җ집лӢҲлӢӨ. к·ёлҰ¬кі мң м Җл“Өмқҙ мғқк°Ғн•ң кІғмқҙ л§һлҠ” кІғмңјлЎң лӮҳнғҖлӮ¬мҠөлӢҲлӢӨ.
3. м•„лӢҲ к·ёлһҳм„ң м–јл§ҲлҸҷм•Ҳ н•ҙм•ј мҪ”мқё лӢӨлӘЁмңјлҠ”лҚ°?
л°© мқёмӣҗмҲҳ л°Ҹ лӮҙк°Җ лӘҮл“ұн• м§Җ м „л¶Җ нҷ•лҘ мқҙ к°ҷлӢӨкі к°Җм •н• кІҪмҡ°мқҳ мҪ”мқён•ЁмҲҳлҠ” лӢӨмқҢкіј к°ҷмҠөлӢҲлӢӨ.
"C(t)=10.223t + 207.607"
мқҙлҹҙ кІҪмҡ° мҪ”мқё 300к°ңлҘј лӘЁмңјлҠ”лҚ° н•„мҡ”н•ң мӢңк°„мқҖ лҢҖлһө нҸүк· 48분 30мҙҲ к°ҖлҹүмңјлЎң лӮҳнғҖлӮ¬мҠөлӢҲлӢӨ.
н•ҳм§Җл§Ң, мӣҗм№ҙл“ң мӢңмһ‘ лҢҖкё° мӢңк°„мқ„ кі л Өн•ҳм§Җ лӘ»н–Ҳкі , 1лҢҖ1л°©мқҙ л“ұмһҘн• нҷ•лҘ мқҙ лҚ” лӮ®кё° л•Ңл¬ём—җ мӢӨм ңлЎңлҠ” нҸүк· 48분ліҙлӢӨ лҚ” л§Һмқҙ кұёлҰҙ кІғмңјлЎң мҳҲмғҒн•©лӢҲлӢӨ.
4. к·ёл ҮлӢӨл©ҙ, л°© мқёмӣҗмҲҳ лі„ мҡ°лҰ¬лҠ” м–ҙл–Ө м „лһөмқ„ м·Ён•ҙм•ј нҳ„лӘ…н•ңк°Җ?В
лӢ№м—°нһҲ л°© мқёмӣҗмҲҳк°Җ м—Ҷмқ„мҲҳлЎқ мӢңк°„мқ„ лҒ„лҠ” кІғмқҙ кё°нҡҢ비мҡ©мғҒ мқҙл“қмһ…лӢҲлӢӨ. мҷңлғҗн•ҳл©ҙ 1л“ұл¶Җн„° 4л“ұк№Ңм§Җ мҪ”мқё мҠөл“қм—җ мһҲм–ҙм„ң л“ұк°„м„ұмқҙ ліҙмһҘлҗҳкё° л•Ңл¬ёмһ…лӢҲлӢӨ. к·ёл Үкё°м—җ 1лҢҖ3мқҳ л°©м—җм„ңлҠ” мөңлҢҖн•ң л№ЁлҰ¬ лҒқлӮҙкі , 1лҢҖ1мқҳ л°©м—җм„ң мөңлҢҖн•ң мӢңк°„мқ„ лҒ„лҠ” кІғмқҙ к°ҖмһҘ мқҙмғҒм Ғмһ…лӢҲлӢӨ.
л§Ңм•Ҫ л“ұк°„м„ұмқҙ ліҙмһҘлҗҳм§Җ м•Ҡм•ҳлӢӨл©ҙ, лӢӨм–‘н•ң мҪ”мқё мҠөл“қ м „лһөмқҙ лӮҳмҷ”мқ„кІҒлӢҲлӢӨ. мқҙ л¶Җ분мқҙ м•„мүҪ
<мҡ”м•Ҫ>
1. мҪ”мқёмқ„ лӢӨ лӘЁмңјлҠ”лҚ° мөңмҶҢ (48분+мӣҗм№ҙл“ң лҢҖкё°мӢңк°„)л§ҢнҒј н•„мҡ”н•ҳлӢӨ.
2. л°© мқёмӣҗмҲҳмҷҖ кҙҖкі„м—Ҷмқҙ мҪ”мқёмқҖ мӢңк°„кіј л“ұмҲҳм—җ мқҳн•ҙ кІ°м •лҗңлӢӨ.
3. л°© мқёмӣҗмҲҳк°Җ м Ғмқ„мҲҳлЎқ мҪ”мқёмқ„ лӘЁмңјкё° мң лҰ¬н•ҳлӢӨ.
4. мҪ”мқёмқҖ 1л“ұ лҢҖ비 2л“ұмқҙ 66.6%, 3л“ұмқҙ 33.3% 4л“ұмқҙ 0%лҘј лЁ№лҠ” кІғмңјлЎң м¶”м •лҗңлӢӨ.
к°ҖлҸ…м„ұ м”№л§қмқҙм§Җл§Ң мқҪм–ҙмЈјм…”м„ң к°җмӮ¬н•©лӢҲлӢӨ.В
4лІҲм—җ лҢҖн•ң кҙҖм°°мқҙ мўҖ м·Ём•Ҫн•ҳкё° л•Ңл¬ём—җ. мқҙлҘј ліҙ충н•ҙм„ң "л°© мқёмӣҗмҲҳлі„ мҪ”мқём „лһө"кёҖмқ„ лӢӨмӢң м“°лҸ„лЎқ н•ҳкІ мҠөлӢҲлӢӨ.В
н‘ңліёлҚ°мқҙн„°лҘј м—…лЎңл“ң мӢӨнҢЁн–ҲмҠөлӢҲлӢӨ.
н‘ңліёмҲҳ집 лҸ„мҷҖмӨҖ мң нғҖм”Ё к°җмӮ¬



 Staregg
Staregg
